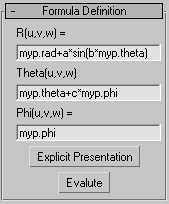
This rollout enables you to add your custom deformation on the base object using three coordinate functions.You should define these function base on coordinate system you have chosen from Coordinate system rollout. In the front example spherical coordinate system has been selected. Therefore the scripts will product Radius, azimuth & longitude of the new point. Basically this functions map the point (x,y,z) of the base object to the point (f(x),g(y),h(z)) in new object. Here u,v & w are corresponding with x,y & z.

The first step to apply a desired deformation on a form is better understanding of it. In this example we considered a sphere as the base object. The sphere can describe by assuming all points with equal distance from a given center point. We can gather all points of the sphere by passing the vertices coordinates into getspherical function. To return the vertices to their original position we need to set functions R,Theta and Phi by the component of the new spherical point.

That means the object has been regenerate in spherical coordinate system. Now we can apply the transformation on the vertices by modifying the current position. In the example above each vertex gets distance from the current position by adding  to the radius component. Parameters <a> and <b> can control the amount and quality of the scaling vertices based on the theta of the point. The result rotates along the Z axis by adding    to theta component. This argument causes rotation of those points that have bigger value of phi. Therefore the points on top and button of the sphere move more than points close to the equator. Because of the Sin function the radius will change periodically and give us the wave effect on the surface. Considering both rotation and scale transformations result looks like a twisted rippled ball.

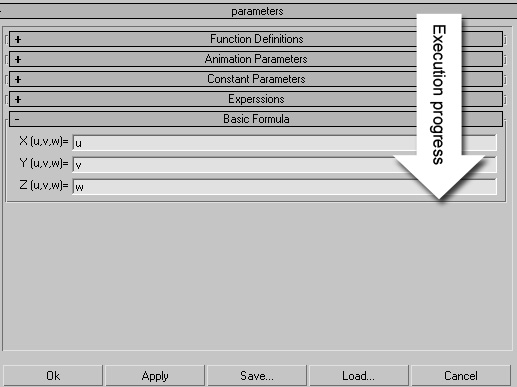This dialog box lets you to create or modify the parameters or customize the functions. Mathsurf provides you an easy way to modify the codes. Any time you make an instance of Mathsurf or reset a parameter program will execute the definitions and commands in order of they located in dialog from up to down.

New: You can save the explicit presentation into a text file and load it into another object using load option available in this dialog.