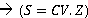A 3d Vector with component of type Complex numbers. Like Point3 value in max-script that represent vectors in 3D space the complex vectors include three components X,Y and Z. the components are complex numbers constructed by Complex class that has mentioned above.

Syntax: “CV = complexVector x y z”

Properties:

<complexVector>.x : first component of complex vector.Return a complex number.

<complexVector>.y : second component of complex vector. Return a complex number

<complexVector>.z : third component of complex vector. Return a complex number

 

Methods:

<complexVector>.re()  : return real part of the complex vector as a point3 value.
If ”CV = complexVector x y z” then
CV.re() = [CV.x.re,CV.y.re,CV.z.re]

<complexVector>.im()  : return imaginary part of the complex vector as a point3 value.
If ”CV = complexVector x y z” then
CV.im() = [CV.x.im,CV.y.im,CV.z.im]

<complexVector>.norm()  : return square of the vector length as complex number.
If “CV = complexVector x y z” then
CV.norm() =  complexVector (x.times (x.conj()))  (y.times (y.conj()))  (z.times (z.conj()))

Operators:

<complexVector>.add z: perform the plus operation with a complex vector or a real 3dvector.

Syntax: CV is complex vector; Z is real vector or complex. S is complex vector:
s = cv.add z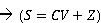

<complexVector>.sub z: perform the minus operation with a real vector or another complex vector and return a new complex vector.

Syntax: CV is complex vector; Z is real vector or complex. S is complex vector:
s = cv.sub z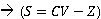

<complexVector>.times z: perform the cross operation with a complex vector  or scalar production with a complex number even a real number.

Syntax: CV and S are complex vectors, if Z is a complex number or a real number the result would be scalar product of Z and CV and if Z is a complexVector the result would be new complex vector that each component are the result of cross product of corresponding components in each given vector.  

s = cv.times z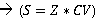

<complexVector>.div z: perform the divide operation with a complex vector  or scalar production with inversion of a complex number even a real number.

Syntax: CV and S are complex vectors, if Z is a complex number or a real number the result would be scalar product of 1/Z and CV and if Z is a complexVector the result would be new complex vector that each component are the result of division of corresponding components in each given vector.  
s = cv.div z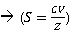

<complexVector>.dot z: return the dot product of two complex vectors. The result is a complex number.

Syntax: CV and Z are complex vectors and S is complex number:
s = c.dot z