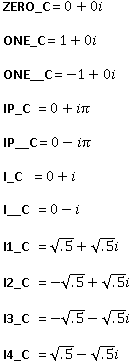In mathematics, the complex numbers are the extension of the real numbers obtained by adjoining an imaginary unit, denoted “i”, which satisfies :
Every complex number can be written in the form a + bi, where a and b are real numbers called the real part and the imaginary part of the complex number, respectively. Mathsurf will add a new variable structure to your 3dsMax script language in form of : ” complex a b” . According to the definition above if “z” is a complex number then   and in max-script the syntax is
“z = complex a b”

Properties:

<Complex>.re: real part of complex number
<Complex>.im: imaginary part of complex number

 

Methods:

<Complex>.denom() : return
<Complex>.r() : return
<Complex>.theta() : return

<Complex>.inverse() : return the inversion.
 if z is a complex number then z.inverse() = 1/z.

<Complex>.conj() : return the conjugation.
The complex conjugate of the complex number z = x + yi is defined to be x − yi,

Operators:

<Complex>.equal z : return true if the complex number and “z” are equal, otherwise return false .

<Complex>.add z: perform the plus operation with a real number or another complex number and return a new complex number.

Syntax: C is complex number; Z is real number or complex. S is complex:
s = c.add z

<Complex>.sub z: perform the minus operation with a real number or another complex number and return a new complex number.

Syntax: C is complex number; Z is real number or complex. S is complex:
s = c.sub z

<Complex>.times z: perform the cross operation with a real number or another complex number and return a new complex number.

Syntax: C is complex number; Z is real number or complex. S is complex:
s = c.times z

<Complex>.div z: perform the divide operation with a real number or another complex number and return a new complex number.

Syntax: C is complex number; Z is real number or complex. S is complex:
s = c.div z

<Complex>.dot z: return the dot product of two complex numbers. The result is a real number.

Syntax: C and Z are complex numbers and S is real:

s = c.dot z

 

More functions:

<Complex>.power (z): return the power of “z” in complex number.

Syntax: C is a complex number; Z is real number and S is Complex:
S=C.power (Z)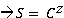

<Complex>.integerpower (n): perform “n” times cross operation on complex number and return new complex number. Use this function instead of Power function if exponent is an integer value.

Syntax: C is a complex number; N is integer number and S is Complex:
S=C.integerpower (N)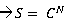

<Complex>. integerRoot(n): return the Nth root of complex number.

Syntax: C is a complex number; N is integer number and S is Complex:
S=C. integerRoot (N)

<Complex>. squareRootNearer(Z):Computes that square root of this complex number that is nearer to previous than to minus previous.

Syntax: C, S and Z are Complex numbers:
S=C. squareRootNearer (Z)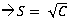

<Complex>.exponential (): return the exponential of complex number.

Syntax: C is a complex number; e is exponent number and S is Complex:
S=C.exponential()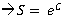

<Complex>. logaritm(): return the logarim of complex number.

Syntax: C and S are Complex numbers:
S=C.logaritm()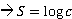

<Complex>.logNearer(z):Computes that complex logarithm of this complex number that is nearest to previous.

Syntax: C, S and Z are Complex numbers:
S=C.logNearer (Z)

Global complex variables:

These variables are global and used to brief complex expressions.