| Torabi Architect. | |
| Implicit Surface Documents | Apr 2009 |
|
||
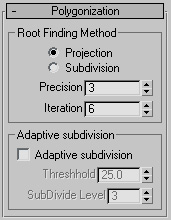
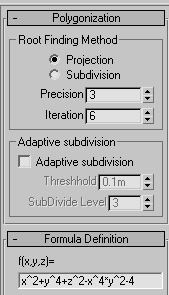
Mathsurf offer two different method for root finding.(basically the surface is result of a progress that aimed to collect all roots of the given equation in specific boundary). The reason of utilizing these two methods in one application is that you can switch between performance and accuracy in each object manually.
|
 |
|
|
||
Projection: the program tries to find the intersection between the surface and each partition by moving the first guessed point toward the surface. This progress performs iteratively until the point lies in a position that absolute result of equation comes less than precision value or maximum iteration occur. Generally the projection method is faster and can produce acceptable result using less iteration. This method uses the first derivative of function that it’s not always easy to calculate therefore it may product some artifact or unacceptable result. Subdivision: the program subdivides the area between each couple of partitions in two different sub-partitions. Then it checks each sub partition and determines which one could possibly contain the root. The algorithm takes the result as argument and the progress runs until the function returns a value less than precision amount or number of subdivision exceed the iteration parameter. Precision: controls the level of accuracy. In fact the those points in space that return the value less than precision value will be considered as root of the equation. 0.1^3 = 0.0001 Iteration: controls how many times the program should redo the root finding progress to achieve the desirable level of accuracy. If the precision meet the criteria before it reaches maximum iteration the rest stages will ignore. |
||
|
||
Example 1: surface took 50.5 seconds in subdivision method and 43.7 seconds in projection method.
|
|
|
|
||
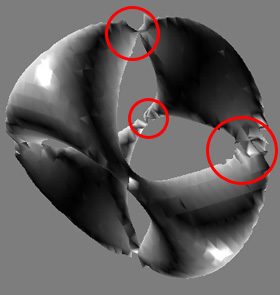
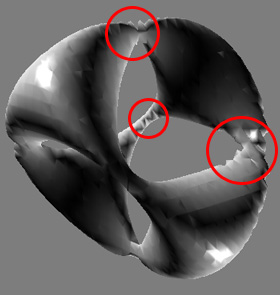
| Example 2: | ||
Bottom Right: unreasonable polygonization by projection method in tiny areas. Process time: 36.053 sec
Front:Implicit setting |
![from [-7,-7,-7] to [7,7,7] subdivisions:[31,31,31]](images/implicit_sample07_setting.jpg) 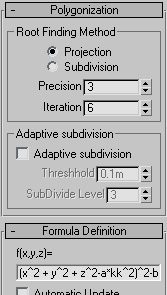 |
|
  |
||
| Adaptive subdivision: | ||
Threshold: If the angle between two faces that sharing an edge is greater than this threshold both faces will subdivide until the intersection angles comes lower than threshold. Subdivide level: controls the level of subdivisions. In some cases implicit surfaces create sharp edges. That means the curvature of surface never goes less than Threshold parameter. To avoid program halting we should limit the level of subdividing. |
||
| Example: | ||
Subdivisions: X: 9 Y: 9 Z: 9 No Adaptive subdivision Object contains 1944 Faces; progress time: 3.5 seconds |
 |
|
Subdivisions: X: 31 Y: 31 Z: 31 No Adaptive subdivision Object contains 23652 Faces; progress time: 31.5 seconds |
 |
|
Subdivisions: X: 9 Y: 9 Z: 9 - Adaptive subdivision applied Threshold: 10, Subdivide level: 3 Object contains 16839 Faces; progress time: 15 seconds |
 |
|
| www.torabiarchitect.com |
![from [-4,4,-4] to [4,4,4] subdivisions:[31,31,31]](images/implicit_sample06_setting2.jpg)
