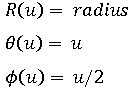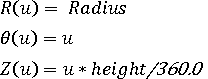Torabi Architect.
Mathcurve Documents Apr 2009
arrowCoordinate System Rollout.

Mathcurve Coordinate Rollout

  

Mathcurve creates the curve using parametric presentation. that means the curve is the result of mapping all points of the interval [uMin,uMax] to 3d space curve via a the specific functions. This mapping can be in different coordinate systems.
arrowCoordinate Systems.

 

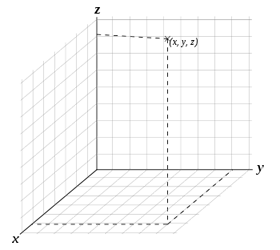
Cartesian:

The curve is described by a map of the interval [uMin,uMax] into Cartezian (x,y,z)-space via the functions X(u) , Y(u) & Z(u).

 

 

   Cartesian Coordinate System

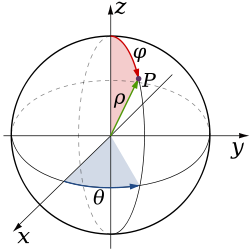
Spherical:

The curve is described by a map of the interval [uMin,uMax] into Spherical (r,θ,φ)-space via the functions R(u),Theta (u) & Phi(u)

   Spherical Coordinate System

Example: the spherical curve C, has been defined by functions:

R(u)=radius,Theta(u)=u,Phi(u)=u/2

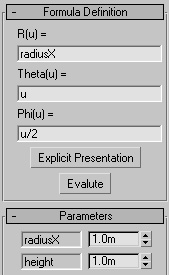   Spherical curve sampleSpherical curve setting

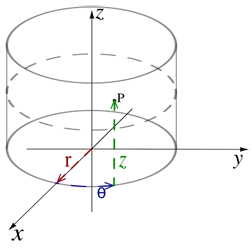
Cylindrical:

The curve is described by a map of a the interval [uMin,uMax] into Cylindrical (r,θ,z)-space via the function R(u),Theta(u) & Z(u)

   Cylindrical Coordinates System

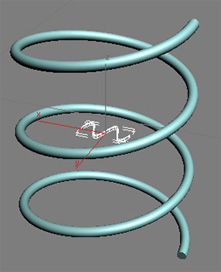
Example: circular helix can describe in cylindrical coordinate by the functions :

R(u) = radius,Theta(u)=u,Z(u)=u*height/360

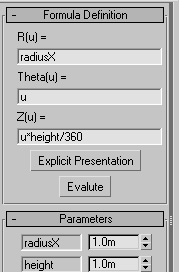   HelixFixed Radius Helix Setting
arrowInterval.
arrowPlug-in features.
arrowBack to Index
 
www.torabiarchitect.com