Mathsurf add some functions into the mathematical function library of max-script which you can use inside or outside of the plug-in.

Round <number>: Returns the nearest whole number to <number>

Example :  
Round 3.7 return 4.0 , round -2.1 return -2.0

Minimum <number1> <number2> :return the smaller number.

Example :  
Minimum -3.0 -5.0 return -5.0

Maximum <number1> <number2> :return the larger number.

Example :  
Maximum -3.0 -5.0 return -3.0

simpsonIntegrator <function> <initial number> <final number> <steps> :

Compute the integral of <function> form <initial number> to <final number> using the Simpson rule.
The interval of [initial,final] will be divided into <steps> segments to approximate the integral amount. Larger value for <steps> provides more accurate result but will take more time to calculate.
Example :   lets   
simpsonIntegrator  f 0.0 2.0 10 return 2.66667

adaptiveIntegrator <function> <initial number> <final number> <approximation>:

Compute the integral of <function> form <initial number> to <final number> using the Adaptive method.  in this method the integrator acts as a recursive function and it recall the function until the approximately value of integral has been achieved. This function will perform more task to compute the integral but it works better for functions that dramatically changes in the given interval.
Example :   lets  
adaptiveIntegrator  f 0.0 2.0 0.0001 return 2.66675

To see the advantage of adaptive method we suppose that

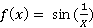
adaptiveIntegrator  f -2.0 1.0 0.0001  return -0.0120755
simpsonIntegrator f -2.0 1.0 10  return  0.0403277
to achive more accurate result we need more steps :
simpsonIntegrator f -2.0 1.0 100  return  0.0123138
simpsonIntegrator f -2.0 1.0 1000  return  -0.0170855
And finally,
simpsonIntegrator f -2.0 1.0 10000  return  -0.0121766
As you can see for this function you need 10000 steps to achieve the same result as Adaptive method.

Minimal surface functions:
Minimal surfaces are defined as surfaces with zero mean curvature. In Mathsurf we parameterize a minimal surface in terms of two functions as

“g” & “h” are functions with name of Hprime and Gauss. These functions are meromorphic  on subset of complex plane. The interval of integral defines by another function we call it domainGrid . this function overrides the default Cartesian grid of (u+iv) into adapted grid .

WeierstrassMinimalSurface <uindex> <vindex> :

This function returns the result of Weierstrass parameterization in specific position of the grid and save the result in HelperArray .when you call WeierstrassMinimalSurface an array will be defined to collect the integral amount in each point. This array will be used in next point to retrieve the previous amount of integral if useHelperArray has set to true. By this trick program can run faster.

createHelperArray () :

This function save all WeierstrassMinimal data for the give interval into helperArray .

helperToMinimal() :

convert the integral value into surface point.

minimalToHelper() :

convert the surface point into integral value .

Getspherical <point3>

This function returns the spherical point of the argument in format of spherical class.
see spherical points.

Example :
getSpherical [2.0,3.0,-3.0] returns (spherical rad:4.69042 theta:56.3099 phi:-39.7622)